The Mandelbrot set

Intricate images of the Mandelbrot set are ubiquitous. You might have seen them randomly featured on your school math textbooks for God knows what reason. They’re probably on the posters of some of math professors in your college. You’ve probably seen some people wearing Mandelbrot set T-shirts or even having Mandelbrot tattoos. Rather than trying to explain its fame, I would like to firstly define this object and state its basic properties.

Definitions

The Mandelbrot set is a subset of the complex plane $\mathbb{C}$. Holly Krieger on numberphile gave a clear and pictorial definition.

In summary, Krieger defined the Mandelbrot set $\mathbb{M}$ as the set of complex parameters $c \in \mathbb{C}$ such that the sequence of iterates of the quadratic map $f_c(z) = z^2 +c$ for the initial value $0$ satisfies $\lvert f^n_c(0) \rvert \leq 2$ for all integers $n \geq 0$.

In the study of holomorphic dynamics, there are a few other equivalent ways of defining the Mandelbrot set.

Proposition $c \in \mathbb{M}$ if and only if it satisfies any of the following equivalent conditions.

1. $\lvert f^n_c(0) \rvert \not\to \infty$ as $n \to \infty$;
2. The filled Julia set $K(f_c)$ of $f_c$ is connected.

The original definition immediately implies 1., and the converse is true as well by elementary analysis. Indeed, if $\lvert c \rvert \leq 2$ and $\lvert z \rvert = 2+ \epsilon$ for some $\epsilon > 0$, then

The inequality shows that if there is some $k$ such that $\lvert f^k_c(0) \rvert = 2 + \epsilon$, then $\lvert f^{k+n}_c(0) \rvert \geq 2 + 4^n \epsilon \to \infty$ as $n \to \infty$. If $\lvert c \rvert = 2 + \epsilon > 2$, then we can show inductively that $\lvert f^n_c(0) \rvert \geq 2 + 3^{n-1} \epsilon$ which again shows divergence to $\infty$.

The second part of the proposition is actually a consequence of the following theorem.

Dichotomy Theorem: For any arbitrary $c \in \mathbb{C}$, either $K(f_c)$ contains $0$ and is connected, or $K(f_c)$ does not contain $0$ and is homeomorphic to the Cantor set.

Refer to my previous post on the definition of the filled Julia set $K(f)$ of a polynomial $f$. The underlying reason behind the theorem is that $0$ is the unique finite critical point of the quadratic map $f_c$. What can you tell about the preimage of a domain under $f_c$ based on whether the domain contains the critical point or not? This is already discussed in another post I made.

Escape Time Algorithm

Each iterate $f^n_c(0)$ is a polynomial of degree $2^{n-1}$ given by

If we let $P_n(c) = f^n_c(0)$, then the Mandelbrot set is defined as the countable intersection of preimages of the closed disk $\mathbb{\mathbb{D}_2}$ of radius 2 centered at 0:

The expression above inspires a straightforward algorithm to produce an image of the Mandelbrot set. Illustrated below is the first few partial intersections.

It isn’t obvious from the gif above that $\mathbb{M}$ is connected. We can actually see this if we make the illustration even fancier. For each time $N \in \mathbb{N}$, we assign a color to the set of parameters $c$ such that $c$ escapes from $\overline{\mathbb{D}_2}$ at the $N^\text{th}$ iterate, i.e. $\lvert f^k_c(0)\rvert \leq 2$ for all $k< N$ but $\lvert f^N_c(0)\rvert \geq 2$. Choosing contrasting colors will help us see the boundary more clearly.

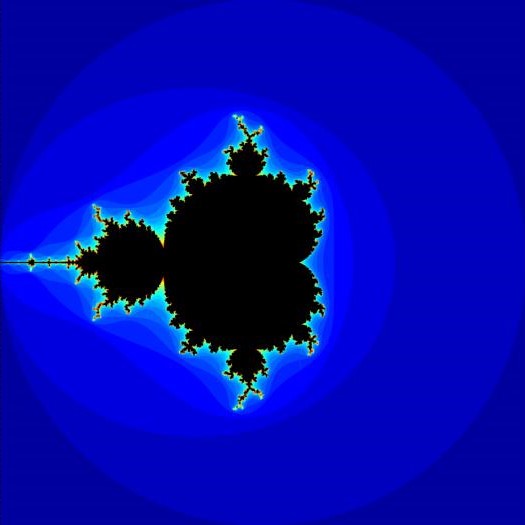
Properties

Looking back at the countable intersection expression above, each of the preimages $P_n^{-1}(\mathbb{D}_2)$ is a compact set containing a common point $0$ since $P_n(0) = 0$ for every $n$. By Cantor’s intersection theorem, we can easily deduce that $\mathbb{M}$ is non-empty and compact. What else can we say about the topology of $\mathbb{M}$?

Theorem: The Mandelbrot set is connected.

Douady and Hubbard proved the connectivity of $\mathbb{M}$ by explicitly constructing a conformal isomorphism $\Phi: \mathbb{C} \backslash \mathbb{M} \to \mathbb{C} \backslash \bar{\mathbb{D}}$. Let’s briefly sketch its construction. For each parameter $c \in \mathbb{C}$, there is a unique holomorphic map $B_c : \mathbb{C} \backslash K(f_c) \to \mathbb{C} \backslash \bar{\mathbb{D}}$ called the Böttcher coordinate such that $B_c \circ f_c (z) = B_c(z)^2$ for all $z \in \mathbb{C} \backslash K(f_c)$. (Refer to Milnor³ $\S 9$.) The equation essentially states that $f_c$ behaves like a doubling map $z^2$ outside the filled Julia set. The map $\Phi(c) = B_c(c)$ is the desired conformal isomorphism. Further details of the proof can be found on Douady and Hubbard’s Orsay notes², Chapter 8.

A central conjecture in holomorphic dynamics is the following.

MLC Conjecture: The Mandelbrot set is locally connected.

Local connectivity of $\mathbb{M}$ has highly important implications. An immediate one is that the conformal isomorphism $\Phi^{-1}$ extends to a continuous map from the unit circle $S^1$ to the boundary $\partial\mathbb{M}$. Topologically, this extension will allow us to obtain a precise topological model of $\mathbb{M}$. Dynamically, MLC implies (in fact, is equivalent to) a strong property called combinatorial rigidity which says that any two quadratics $f_c$ and $f_{c’}$ having no non-repelling periodic points have the same combinatorics if and only if $c = c’$. Ultimately, MLC implies one of the most important open problems in holomorphic dynamics. (Refer to Benini’s survey¹.)

Density of Hyperbolicity Conjecture: The set of parameters $c \in \mathbb{M}$ such that $f_c$ is hyperbolic is dense in $\mathbb{M}$.

We say that $c \in \mathbb{M}$ is a hyperbolic parameter if $f_c$ has a finite attracting periodic point. The Julia sets of hyperbolic maps are nice to deal with since they have zero area and are locally connected. (Refer to Milnor³ $\S 19$.) I will discuss more on hyperbolicity and the Mandelbrot set in future posts.

References

1: A. M. Benini. A Survey on MLC, Rigidity and Related Topics. arXiv: Dynamical Systems, 2017.
2: A. Douady, J. Hubbard. Exploring the Mandelbrot set. The Orsay Notes. Available at http://pi.math.cornell.edu/~hubbard/OrsayEnglish.pdf
3: J. Milnor. Dynamics in One Complex Variable. Princeton University Press, third edition, 2006.