Continuous extension of Riemann mappings and local connectivity
Published:
Given a conformal isomorphism $f: \mathbb{D} \to U$ from the unit disk $\mathbb{D}$ to a simply connected domain $U$ embedded in the Riemann sphere $\mathbb{P}^1$, one may ask whether or not $f$ can be continuously extended to the boundary of $U$. The answer depends solely on the topology of the domain $U$.
The main theorem I would like to highlight in this post is the following.
Carathéodory-Torhorst Theorem: Let $f$ be a Riemann mapping $f: \mathbb{D} \to U$. The following statements are equivalent.
- $f$ extends continuously to a map from $\bar{\mathbb{D}}$ onto $\bar{U}$;
- $\partial U$ is a closed curve, i.e. the image of a continuous map $\partial \mathbb{D} \to \mathbb{P}^1$;
- $\partial U$ is locally connected;
- $\mathbb{P}^1\backslash U$ is locally connected.
Local connectivity
There are many different ways to define local connectivity of a space $X$. We say that a Hausdorff space $X$ is locally connected if every point $x \in X$ admits an arbitrarily small connected neighborhoods. When $X$ is a compact metric space (e.g. a compact subset of $\mathbb{P}^1$), we can also say that $X$ is locally connected if for all $\epsilon >0$, there is some $\delta = \delta(\epsilon) >0$ such that every pair of points $x$ and $y$ in $X$ which satisfy $d(x,y) < \delta$ admits a connected subset $K \subset X$ containing $x$ and $y$ of diameter $< \epsilon$.
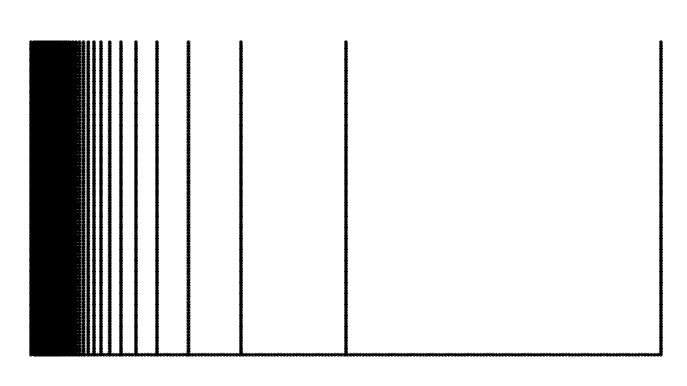
Examples of locally connected compact sets include Jordan arcs and Jordan curves. (Yes… Koch snowflake is included.) An example of a connected set that is not locally connected coming from standard undergraduate classes in topology would be the closure of the topologist’s sine curve $\{ (x,\sin(1/x) ) : \vert : x>0 \} \cup \{0 \} \times [-1,1]$. The closure of $[0,1] \times \{ 0\} \cup \bigcup_{n\geq 1} \{\frac{1}{n} \} \times [0,1]$ is not locally connected at any point on the vertical segment $\{0\} \times [0,1]$. The latter is called the comb space, and it is illustrated in the figure below.
Crosscuts
Carathéodory introduced the theory of prime ends to study the boundary behaviour of conformal maps. Here, I will attempt to give a brief summary based on the books of Milnor1 and Pommerenke2.
A crosscut $C$ of $U$ is an embedded closed arc $[0,1] \to \bar{U}$ such that the intersection $C \cap \partial U$ consists of exactly the two endpoints of $C$. A crosscut of U always divides $U$ into two, one of which will be called a crosscut neighborhood $N$ of $C$.
An infinite sequence of crosscut neighbhorhoods $\{ N_n \}_{n\geq 0 }$ of $\{ C_n \}_{n\geq 0}$ is a chain if
- for all $n\geq 0$, $N_{n+1} \subset N_n$;
- in spherical metric, $\text{diam} \bar{C_i} \to 0$ as $i\to \infty$;
- the crosscuts $C_n$ are all pairwise disjoint.
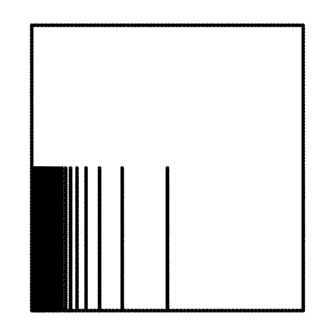
The impression of a chain $\{N_n \}_{n\geq 0 }$ is $I = \cap_{n \geq 0} \bar{N_n}$. By Cantor’s intersection theorem, the impression $I$ is always a non-empty compact connected set. For example, if $U$ is the bounded domain with boundary $\partial U$ being the union of the comb space we mentioned before and the boundary of $[0,1] \times [0,2]$ as shown below, and if we have a chain induced by the crosscuts which are the red line segments shown below, then the impression is the left segment $\{0\} \times [0,2]$.
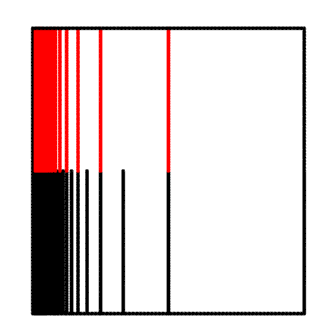
We can apply the terms we just introduced above for our purposes as follows. For every point $a$ on the unit circle $\partial \mathbb{D}$, it is easy to construct a chain in $\mathbb{D}$ whose impression is $a$ (e.g. consider the intersection of arbitrarily small disks centered at $a$ and $\mathbb{D}$). In fact, there is always a chain $\{ C_n \}$ in $\mathbb{D}$ such that its impression is $a$ and its image $\{ f(C_n) \}$ is also a chain. (The non-trivial step here is to show that the crosscuts $f(C_n)$ are pairwise disjoint. Refer to Milnor Lemma 17.9 for more details.)
How would this all help us in extending $f$ to the boundary? The impression $I$ of the chain $\{ f(C_n) \}$ encodes the set of possible limits of $f(z)$ as $z \in \bar{U}$ converges towards $a$. If the impression of $\{ f(C_n) \}$ is a singleton $w \in \partial U$, then $f$ extends continuously at $z$ and $f(z)=w$. Hence, $f$ can be continuously extended to the boundary if the boundary of $U$ has ‘good’ topology, i.e. the impression of every chain of $U$ is a singleton.
Carathéodory-Torhorst Theorem
Suppose $f$ does extend continuously to the boundary. Clearly, $\partial U$ is a closed curve because $f$ induces a continuous surjection from $\partial \mathbb{D} \to \partial U$. Since closed curves are always locally connected, 2. also immediately implies 3.
Suppose $\partial U$ is locally connected. If a point $x$ lies in the interior of $\mathbb{P}^1 \backslash U$, it is immediate that $x$ will always have arbitrarily small connected open neighborhoods. Hence, let’s pick a point $x$ on $\partial U$ and check that $\mathbb{P}^1 \backslash U$ is locally connected at $x$. Pick any small open neighborhood $V \subset \mathbb{P}^1$ of $x$. By local connectivity of $\partial U$, there is an open connected subset $K$ of $V \cap \partial U$ containing $x$. There is an open disk $D \subset V$ such that $x \in D \cap \partial U \subset K$. Therefore, $K \cup (D \cap U)$ is a connected neighborhood of $x$. This shows that $\mathbb{P}^1 \backslash U$ must be locally connected as well.
It remains to show that 4. implies 1. We will show that the impression of every chain in $U$ must be a singleton. Pick any chain $\{ N_n\}$ with crosscuts $\{ C_n \}$. Pick $\epsilon >0$ and let $\delta = \delta(\epsilon) >0$ be from the definition of local connectivity of $\mathbb{P}^1 \backslash U$. When $\text{diam} (C_n) \leq \delta$, the endpoints of $C_n$ are $\leq \delta$ apart and therefore contained in a connected subset $X_n$ of $\mathbb{P}^1 \backslash U$ of diameter $< \epsilon$. The union $C_n \cup X_n$ bounds a region containing the neighborhood $N_n$. As $\epsilon + \delta$ can be arbitrarily small and as $\text{diam} (\bar{N_n}) \leq \text{diam} (C_n \cup X_n) \leq \epsilon + \delta$, the impression $\cap \bar{N_n}$ must be a singleton.
Jordan Domains
When our domain $U$ is a Jordan domain, we can say more about the behaviour of $f$ on the boundary.
Carathéodory Theorem: Let $f$ be a Riemann mapping $f: \mathbb{D} \to U$. Then, $f$ extends continuously to a homeomorphism from $\bar{\mathbb{D}}$ onto $\bar{U}$ if and only if $U$ is a Jordan domain.
Following Carathéodory-Torhorst theorem, we only need to check that the continuous extension $f: \partial \mathbb{D} \to \partial U$ is a homeomorphism when $U$ is a Jordan domain. Actually, by topological reasons, it is sufficient to check that $f$ is injective on $\partial \mathbb{D}$. When $f(a)=f(b)=z_0$ for some pair of points $a \neq b$ on $\partial \mathbb{D}$, the image $f(L)$ of the hyperbolic geodesic $L$ in $\mathbb{D}$ with endpoints $a$ and $b$ is a curve in $ U$ which starts and ends at $z_0$. The closure $\overline{f(L)}$ is a Jordan curve bounding a region $V$ and $V$ must contain $f([a,b])$ where $[a,b]$ denotes an arc in $\partial \mathbb{D}$ with endpoints $a$ and $b$. Since $U$ is a Jordan curve, $f([a,b])$ has to be the singleton $\{ z_0 \}$. We can then apply the Schwarz reflection principle to show that $f$ must be constant. This is a contradiction, and therefore $f$ must be injective on the boundary.
References
1: J. Milnor. Dynamics in One Complex Variable. Princeton University Press, third edition, 2006.
2: C. Pommerenke. Boundary Behaviour of Conformal Maps. Springer-Verlag, Berlin Heidelberg, 1992.