Classification of Riemann surfaces

The uniformisation theorem states that every simply connected Riemann surface $X$ is conformally isomorphic to either the unit disk $\mathbb{D}$, the complex plane $\mathbb{C}$ or the Riemann sphere $\mathbb{P}^1$. The classical proof relies heavily on techniques in potential theory including the Dirichlet principle and the Perron method. (Refer to Forster’s book³.) Rather than discussing the proof in detail, I am more interested in some of the immediate applications of the uniformisation theorem. This includes classification of Riemann surfaces in general.

Let’s review a bit of covering space theory. Every connected Riemann surface $X$ admits a universal cover $p : Z \to X$, unique up to homeomorphism. The space $Z$ can be endowed with the pullback complex structure from $X$ such that $Z$ is a simply connected Riemann surface and $p$ is holomorphic. Consequently, with respect to this complex structure, the deck transformations of $p$ are automatically conformal automorphisms of $Z$ forming a subgroup $\Gamma$ of the group $\text{Aut}(Z)$ of all conformal automorphisms of $Z$. Surely, $\Gamma$ must be a discrete subgroup acting freely and properly discontinuously on $Z$.

The goal for now is to see what $\Gamma$ looks like for every possible $Z$. This will help us see what kind of Riemann surfaces have which universal covers. We will say that $X$ is elliptic/spherical if it is covered by $Z = \mathbb{P}^1$, Euclidean/parabolic if $Z = \mathbb{C}$, and hyperbolic if $Z = \mathbb{D}$.

Elliptic Riemann surfaces

Suppose $Z$ is the Riemann sphere. A result in complex analysis states that every holomorphic self map of the Riemann sphere is a rational map $p(z)/q(z)$ where $p$ and $q$ are polynomials. Consequently, the group $\text{Aut}(\mathbb{P}^1)$ of conformal automorphisms of $\mathbb{P}^1$ has to be the group of Möbius transformations, often denoted as $PSL(2,\mathbb{C})$:

A simple algebraic exercise should convince you that every Möbius transformation has a fixed point. As such, every subgroup $\Gamma$ of $\text{Aut}(\mathbb{P}^1)$ does not act freely on $\mathbb{P}^1$ unless $\Gamma$ is the trivial group consisting only of the identity map. Therefore, every connected Riemann surface $X$ which admits a universal cover $\mathbb{P}^1$ must be $\mathbb{P}^1$ itself!

Parabolic Riemann surfaces

Suppose $Z$ is the complex plane. Every conformal automorphism $f \in \text{Aut}(\mathbb{C})$ can be extended to a conformal automorphism of $\mathbb{P}^1$ by applying Riemann’s theorem of removable singularities. The extension must have a fixed point at $\infty$ and the only Möbius transformations fixing $\infty$ are linear maps. In short,

Since we are only interested in subgroups acting freely, we only care about non-identity elements without fixed points, namely translations $\gamma_b(z) = z+b$ where $b\neq 0$. Another simple algebraic exercise should convince you that every translation is conjugate to each other in $\text{Aut}(\mathbb{C})$, so then we may as well assume that $\Gamma$ contains the real unit translation $\gamma_1$ and every other non-identity element $\gamma_c$ in $\Gamma$ satisfies $|c|\geq 1$. We shall consider two non-trivial cases:

• $\Gamma$ is generated by $\gamma_1$. This produces a bi-infinite cylinder conformally isomorphic to the punctured plane $\mathbb{C}^*$ by the map $\mathbb{C}/\Gamma \to \mathbb{C}^*, z \mapsto e^{2\pi i z}$.
• $\Gamma$ contains some $\gamma_b$ where $b \not\in \mathbb{Z}$ and $|b|\geq 1$. The value $b$ cannot be real for otherwise there is an integral linear combination of $1$ and $b$ that has absolute value less than $1$. $\Gamma$ cannot contain an element $\gamma_c$ where $c$ is in $\mathbb{Z} + b\mathbb{Z}$, i.e. $c$ is an integral linear combination of $1$ and $b$, for otherwise $\Gamma$ would not be discrete. $\mathbb{Z} + b\mathbb{Z}$ form a discrete lattice on $\mathbb{C}$; if $\Gamma$ is generated by $\gamma_1$ and $\gamma_b$, then $X$ is a (complex) torus, often denoted by $\mathbb{C} / \mathbb{Z} + b\mathbb{Z}$. As such, every parabolic Riemann surface is conformally isomorphic to either the plane $\mathbb{C}$, the punctured plane $\mathbb{C}^*$ or a complex torus. The only compact one is the latter.

I have to emphasise that a topological torus can support infinitely many complex structures. Suppose we have a conformal isomorphism $f : \mathbb{C} / \mathbb{Z} + b\mathbb{Z} \to \mathbb{C} / \mathbb{Z} + c\mathbb{Z}$ between two tori where $b$ and $c$ are assumed to be on the upper half plane $\mathbb{H}$. This map lifts to a conformal automorphism $g$ of $\mathbb{C}$ fixing $0$ — hence, of the form $g(z) = \alpha z$ — such that $g$ restricts to an isomorphism from the lattice $\mathbb{C} / \mathbb{Z} + b\mathbb{Z}$ to the lattice $\mathbb{C} / \mathbb{Z} + c\mathbb{Z}$. Therefore, there are integers $p,q,r,s \in \mathbb{Z}$ such that

In other words, $c = h(b)$ where $h(z) = \frac{pz+q}{rz + s}$. The map $h$ must be invertible because $g$ is invertible, so then $h$ lies in the modular group $PSL(2,\mathbb{Z})$. The group $PSL(2,\mathbb{Z})$ is a discrete subgroup of $\text{Aut}(\mathbb{H})$ (we shall see more of $\text{Aut}(\mathbb{H})$ below) and since the set of orbits $\mathbb{H} / PSL(2,\mathbb{Z})$ is infinite, a torus can have infinitely many complex structures.

Hyperbolic Riemann surfaces

It then follows from above that a Riemann surface $X$ must be hyperbolic if it is not conformally isomorphic to $\mathbb{P}^1$, $\mathbb{C}$, $\mathbb{C}^*$ or a complex torus. We will first look at a few special cases:

• Suppose $X$ is a compact Riemann surface of genus $g$. If $g \geq 2$, then it is not homeomorphic to the sphere $\mathbb{P}^1$ nor the torus. Thus, $X$ admits a hyperbolic complex structure.
• Suppose $X$ is a two-punctured plane, then it must be hyperbolic since it is clearly topologically different from elliptic or parabolic Riemann surfaces. This fact has an important consequence.

Little Picard Theorem: The image of a non-constant entire function is either $\mathbb{C}$ or $\mathbb{C}\backslash \{p\}$ for some point $p$.

Indeed, if a non-constant entire function $f$ omits two values $p$ and $q$, then we can lift $f$ to a non-constant entire map $f_1 : \mathbb{C} \to \mathbb{D}$ via the universal cover $\mathbb{D} \to \mathbb{C}\backslash\{p,q\}$. However, such a lift $f_1$ should not exist by Liouville’s theorem. (See Ahlfors¹ Chapter 8 $\S 3$ for another proof.)

• Suppose $X$ is a domain in $\mathbb{C}$ such that $\mathbb{C} \backslash X$ contains more than 2 points. Clearly, $X$ is not elliptic because it is not compact and, by Little Picard theorem, $X$ cannot be parabolic. Therefore, $X$ is a hyperbolic Riemann surface.

To obtain more concrete examples, let’s consider discrete subgroups of $\mathbb{D}$. A consequence of Schwarz Lemma is that this group is just the group of degree 1 Blashcke products:

It is often easier to work with the upper half plane model. With the aid of conformal automorphism $\Phi : \mathbb{H} \to \mathbb{D}, z \mapsto \frac{i-z}{i+z}$, we can obtain $\text{Aut}(\mathbb{H})$ by working out $\Phi^{-1} \text{Aut}(\mathbb{D}) \Phi$. This turns out to be the group $PSL(2,\mathbb{R})$:

Notice that $\text{Aut}(\mathbb{H})$ is a subgroup of $\text{Aut}(\mathbb{C})$ consisting of all Möbius transformations preserving the upper half plane. Every element that has no fixed point in $\mathbb{H}$ turns out to be conjugate to either a translation $\sigma_{\pm}(z) = z \pm 1$ or a dilation $\tau_a(z) = az$ where $a>1$. Let $X$ be a hyperbolic Riemann surface with covering group $\Gamma$, a discrete subgroup of $\text{Aut}(\mathbb{H})$ acting freely and properly discontinuously.

• When $\Gamma$ is generated by $\sigma_{+}$, the quotient $X$ is a semi-infinite cylinder conformally isomorphic to the punctured disk $\mathbb{D}^*$ by the map $X \to \mathbb{D}^*, z \mapsto e^{2\pi i z}$.
• When $\Gamma$ is generated by $\tau_a$ for some $a>1$, the quotient $X$ is an annulus conformally isomorphic to the regular concentric annulus $A = \{ e^{-2\pi^2/\ln a} < \lvert z \rvert <1 \}$ by the map $X \to A, z \mapsto z^{2\pi i/\ln a}$.

Similar to the torus case, a topological annulus admits infinitely many complex structures. Using the notation $A_r = \{ 1<\lvert z\rvert < r \}$ for any $r>1$, let $f: A_r \to A_s$ be a conformal isomorphism mapping the inner boundary of $A_r$ to the inner boundary of $A_s$. The map $f$ lifts to a conformal automorphism $g \in \text{Aut}(\mathbb{H})$ which maps the negative (resp. positive) real axis onto itself, so then $g = \tau_\alpha$ for some $\alpha >0$. However, by invariance under deck transformations of $f$ and $f^{-1}$, we must have the equation $f(az) = bf(z)$ where $a = e^{2\pi^2/\ln r}$ and $b = e^{2\pi^2/\ln s}$. This forces $r$ to be equal to $s$. As such, two concentric annuli are conformally isomorphic if and only if they have the same ratio of outer to inner radii.

More complicated hyperbolic Riemann surfaces arise when $\Gamma$ has at least two generators. The possibility is rather endless, but the least I can do is give one more example. Suppose $\Gamma$ is generated by the dilation $\tau_2$ and the conformal automorphism $\phi(z) = \frac{2z+1}{z+2}$. It turns out that $\Gamma$ is a free group and the quotient $X$ is a punctured torus.

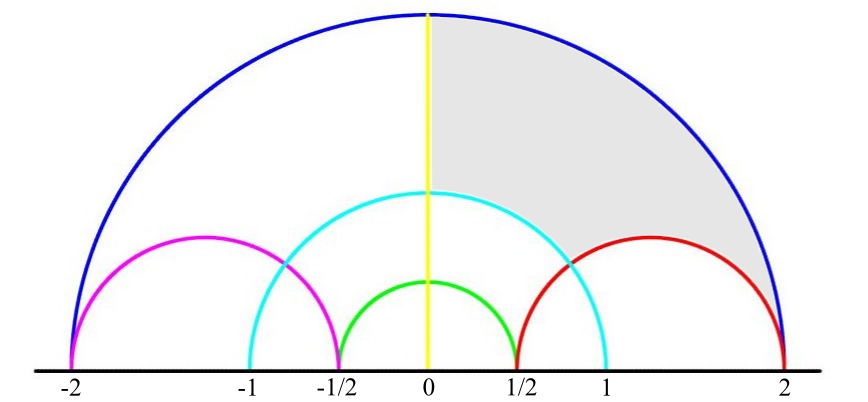
The function $\tau_2$ fixes $0$ and $\infty$, preserves the positive imaginary axis in yellow, and maps the green semicircle to the cyan semicircle, and the latter to the blue semicircle. Meanwhile, the function $\phi$ fixes $\pm 1$, preserves the cyan semicircle, and maps the purple semicircle to the positive imaginary axis in yellow, and then to the red semicircle. As the blue and cyan semicircles are glued together, and so are they yellow ray and the red semicircle respectively, the gray region becomes a fundamental domain of $\Gamma$. The non-existent vertex at the point $2$ gives us the puncture in the torus obtained after gluing. Since a punctured torus deformation retracts onto a bouquet of two circles, its fundamental group must be a free group of two generators.

References

1: L. Ahlfors. Complex Analysis. McGraw-Hill, 1979.
2: L. Ahlfors. Conformal Invariants: Topics in Geometric Function Theory. AMS Chelsea Publishing, 1973.
3: O. Forster. Lectures on Riemann surfaces. Graduate Texts in Mathematics, Vol 81. Springer-Verlag, NY-Berlin, 1981.
4: J. H. Hubbard. Teichmüller Theory and Applications to Geometry, Topology, and Dynamics. Vol. 1. Matrix Editions, Ithaca, NY, 2006.