Classification of Fatou components

Given a holomorphic endomorphism $f: X \to X$ of a Riemann surface $x \in X$, one often studies the dynamics of $f$ by splitting $X$ into the Fatou set $F(f)$ and the Julia set $J(f)$. In this post, we discuss the classification of Fatou components based on the dynamical behaviour of $f$ within.

The Fatou set $F(f)$ is defined to be the open set of points $z \in X$ such that there is a neighbourhood of z on which $\{f^n\}_{n \in \mathbb{N}}$ is a normal family (or equivalently, locally equicontinuous with respect to some natural metric). The Julia set $J(f)$ is precisely the complement of $F(f)$. One may think of $F(f)$ as the maximal region of stability of $f$, and $J(f)$ as the closed set where $f$ behaves chaotically. (See this post for more details.)

Montel’s theorem tells us that the iterates $\{f^n\}$ of an endomorphism $f$ of any hyperbolic Riemann surface always forms a normal family, so then $J(f)$ is empty. Actually, we already have a complete dynamical classification for endomorphisms of a hyperbolic Riemann surface (and in particular the unit disk $\mathbb{D}$) here. This leaves us with non-hyperbolic Riemann surfaces.

The local behaviour of $f$ often gives us a great deal of information on $F(f)$ and $J(f)$. In particular, when $x$ is a periodic point of some period $p$, i.e. $f^p(x)=x$, the derivative $\lambda = \vert (f^p)’(x)\vert$ dictates the behaviour of $f$ near $x$. We say that $x$ is attracting if $\vert \lambda \vert =1$, neutral if $\vert \lambda \vert =1$, and repelling if $\vert \lambda \vert > 1$. In the neutral case, $x$ is parabolic or rationally indifferent if the argument $\text{arg}(\lambda)$ is rational, and irrationally indifferent if $\text{arg}(\lambda)$ is irrational. The Julia set is precisely the closure of the set of repelling periodic points of $f$.

Let’s assume that $f$ is not an automorphism. In this case, it turns out that repelling periodic points always exist and the Julia set $J(f)$ is always non-empty. Let’s also assume that $J(f)$ is not the whole $X$ (this always happens if $X$ is a complex torus; see here), so then the Fatou set $F(f)$ is a non-empty proper subset of $X$.

Classification of periodic components

Suppose $U$ is a connected component of $F(f)$. $U$ is called pre-periodic if there are some $m, p \in \mathbb{N}$ such that $f^m(U) = f^{m+p}(U)$. The minimum possible $n$ is called the period of $U$ and the minimum possible $m$ is called the pre-period of $U$. Roughly speaking, after $m$ iterates, $f^m (U), f^{m+1}(U), \ldots f^{m+p-1}(U)$ form periodic cycle of period $n$.

We have a complete classification of periodic Fatou components.

Theorem: If $U$ is a periodic component of $F(f)$ of period $p$, exactly one of the following holds:

1. $U$ is an attracting basin: there is an attracting periodic point $x \in U$ of period $p$ and for all $y \in U$, $f^{np}(y) \to x$ as $n \to \infty$.
2. $U$ is a parabolic basin: there is a parabolic periodic point $x \in \partial U$ of period $p$ and for all $y \in U$, $f^{np}(y) \to x$ as $n \to \infty$.
3. $U$ is a Baker domain: there is an essential singularity $x \in \partial U$ such that for all $y \in U$, $f^{np}(y) \to x$ as $n \to \infty$.
4. $U$ is a Siegel disk: there is a conformal conjugacy $\phi: U \to \mathbb{D}$ such that $\phi\circ f^p \circ \phi^{-1}(z) = e^{2 \pi i \theta} z$ for some irrational $\theta$.
5. $U$ is a Herman ring: there is a conformal conjugacy $\phi: U \to \{ r < \vert z \vert < R \}$ for some $0<r<R <\infty$ such that $\phi\circ f^p \circ \phi^{-1}(z) = e^{2 \pi i \theta} z$ for some irrational $\theta$.

You may notice that this very much follows from the classification on hyperbolic Riemann surfaces. There are a number of key takeaways:

• Every Fatou component $U$ is always either a basin of attraction or a rotation domain.
• Baker domains and Herman rings are the only types which do not come from a periodic point.
• Baker domains do not exist when $X =\mathbb{P}^1$. This is because $f$ would always be a rational map of the form $p(z)/q(z)$ for some polynomials $p$ and $q$ and essential singularities do not exist. When $X$ is elliptic (isomorphic to the plane $\mathbb{C}$ or the punctured plane $\mathbb{C}\backslash \{0\}$), the points $0$ and $\infty$ are possible essential singularities and Baker domains may exist.
• When $f$ is an entire function on $\mathbb{C}$, every bounded Fatou component $U$ is simply connected. Indeed, by the maximum principle, $f$ would map the union $V$ of $U$ and the bounded component of the complement of $U$ into itself, but since $V$ is hyperbolic as a Riemann surface, Montel’s theorem tells us that the whole $U$ had to lie in the Fatou set. In particular, entire functions never have any Herman ring.

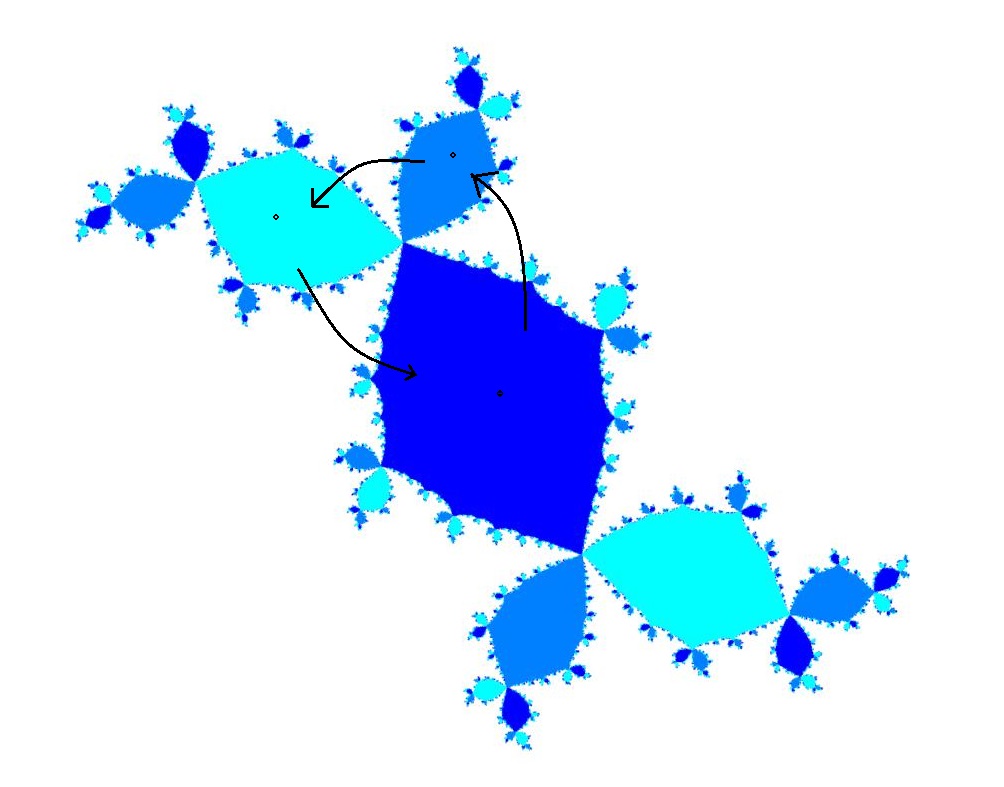
Below is an example of periodic Fatou components. The quadratic $f(z)=z^2 -0.12+0.75i$ admits a cycle attracting periodic points of period $3$ lying inside a periodic cycle of attracting basins permuted according to the arrows. Other colored Fatou components are preimages of this periodic cycle of Fatou components. The white region outside is in fact a fixed attracting basin of $\infty$ in which points diverge to $\infty$ under iterations.

Wandering domains

If not pre-periodic, $U$ is called wandering. This is when $f^m(U)$ and $f^n(U)$ are always disjoint for all distinct positive integers $m$ and $n$. One of the most celebrated results in one-dimensional holomorphic dynamics is the following.

Sullivan’s No Wandering Domains Theorem: If $f(z) = p(z)/q(z)$ is a rational map on $\mathbb{P}^1$, every Fatou component is pre-periodic.

The theorem was initially conjectured by Fatou himself. The proof by Dennis Sullivan was one of the first instances in which the theory of quasiconformal maps was applied in the field of holomorphic dynamics. The intuition is the following: if $U$ were a wandering Fatou component of a degree $d$ rational map, then it would support an infinite dimensional space of Beltrami forms and therefore an infinite dimensional family of distinct rational maps which are quasiconformally conjugate to $f$ itself, contradicting the finite dimensionality of the space of all rational maps of degree $d$.

If $f$ admits a wandering Fatou component, then the underlying space $X$ is the complex plane $\mathbb{C}$ or the punctured plane $\mathbb{C}\backslash \{0\}$ and the map $f$ is transcendental: it can be represented as an infinite power series $\sum_{n= -\infty}^\infty a_n z^n$ which converges everywhere and $a_n$ are not $0$ for infinitely many $n\geq 0$. One may ask if there is a way of completely classifying the dynamics of $f$ on wandering domains. There has recently been significant progress² in this direction. When the domain is simply connected, we can classify them in terms of the hyperbolic distances between different iterates in the domain and the behaviour of orbits relative to the boundary of the domain.

References

1: A. Beardon. Iteration of Rational Functions. Grad. Texts Math. 132, Springer-Verlag, NY, 1984. 2: A. M. Benini, V. Evdoridou, N. Fagella, P. J. Rippon, G. M. Stallard. Classifying simply connected wandering domains. Mathematische Annalen, 2021.
3: J. Milnor. Dynamics in one complex variable. Princeton University Press, third edition, 2006.